SELM: Symmetric Encryption with Language Models

Research by Samuel Stevens & Yu Su

We're excited to present our encryption algorithm SELM, a novel symmetric encrytion algorithm based on language models' incredible ability to memorize data. While SELM is not amenable to conventional cryptanalysis, we investigate its security through an empirical variant of the classic IND-CPA game.

Paper Code

Hundred-Mile Overview [permalink]

This overview assumes at least a passing familiarity with autoregressive language models, machine learning, symmetric encryption, and the IND-CPA game. The later sections present everything without any assumed background.

Large language models (LMs) pre-trained on large text corpora often memorize data seen during pretraining, which compromises language quality [Lee et al., 2022] and can reveal private data in the pretraining corpora [Carlini et al., 2021]. Because of this, we typically consider LM memorization a problem to be solved [Bommasani et al., 2021].

We frame LM memorization as a under-explored skill and develop SELM, a symmetric encryption algorithm with autoregressive languge models.

Alice sends a message to Bob by fine-tuning a public language model in a secret subspace (parameterized by the secret key k) of the original parameter space to memorize her message m. She sends the change in parameters in the secret subspace to Bob, who converts them from the secret subspace to the original parameter space using the secret key k, and decodes the original message. Eve can't read the message because she can't convert from the secret subspace to the original parameter space.

We empirically investigate (1) whether LMs can encrypt all arbitrary data while constrained to subspace optimization and (2) SELM's security by training binary classifiers to play the IND-CPA game. We find that LMs (surprisingly) can memorize any abritrary data, even constrained to only thousands of free parameters, and that regularization is necessary to prevent simple classifiers from winning the IND-CPA game.

The rest of this blog post is less dense and has examples, pictures and interactive widgets to develop intuition around our work.

Table of Contents

1. Hundred-Mile Overview
2. Introduction to SELM
3. Can LMs Memorize Everything?
4. Interlude: Semantic Security
5. SELM's Security
6. Why Does This Matter?
7. (Optional) Beginner Introduction to Symmetric Encryption

Demos, Figures & Tables

1. Animated Overview
2. Intrinsic Dimension Intuition (Demo)
3. What Affects LM Memorization (Figure)
4. Caesar Cipher Semantic Security (Demo)
5. SELM L2 Norm. Distribution (Figure)
6. L2-normalized SELM L2 Norm. Distribution (Figure)
7. Distribution-Regularized SELM L2 Norm. Distribution (Figure)
8. SELM L2 Norm. Distribution (Figure)
9. Security Results with Summary Statistics (Table)
10. Security Results with the Cipher (Table)
11. Caesar Cipher (Demo)
12. Learning From Ciphertext Intuition (Demo)

Introduction to SELM [permalink]

SELM is our novel symmetric encryption algorithm that uses large language models (like GPT) to encrypt arbitrary data.

In a naive formulation of SELM, when Alice wants to send Bob a message, she would directly fine-tune a public pre-trained language model with \(D\) pre-trained parameters \(\theta^D_0\) to memorize her message \(m\):

After fine-tuning, she would have a parameter update vector \(\Delta \theta^D\): $$\Delta \theta^D = \theta^D_* - \theta^D_0$$ Then she could send Bob the update vector \(\Delta \theta^D\). Bob would simply add the vector to the public pre-trained model: $$\theta^D_0 + \Delta \theta^D = \theta^D_*$$ Then Bob could autoregressively generate text from the tuned language model, and he is guaranteed to generate Alice's original message.

There are two problems:

1. The vector \(\Delta \theta^D\) is very large (it's the same size as the original language model).
2. More importantly, Eve can also add \(\Delta \theta^d\) to the public pre-trained language model and read Alice's message.

Instead of minimizing loss with respect to \(\theta^D\), we project a much smaller vector \(\theta^d\) into the \(D\)-dimensional space via a secret projection \(P_k : \mathbb{R}^d \rightarrow \mathbb{R}^D\), then minimize loss with respect to this smaller vector \(\theta^d\). Then Alice sends the optimized \(\theta^d_*\) to Bob, who uses the secret projection \(P_k\) to project \(\theta^d_*\) back to original parameter space, which he adds to the public pre-trained LM parameters: $$P_k(\theta^d_*) + \theta^D_0 = \theta^D_*$$

This elegantly solves both problems at once:

1. The vector \(\theta^d_*\) is much smaller (upwards of 100,000x) than the original vector \(\theta^D_*\).
2. Eve can't project the smaller vector \(\theta^d_*\) into the LM's parameter space because the projection \(P\) is parameterized by the secret key \(k\) that only Alice and Bob share.

If this idea of secret subspace optimization is unclear, don't worry! We have a toy example where you can play with all the different variables in 2- and 3-D until you have a better feel for what SELM is all about.

Suppose that \(D = 3\) and \(d = 2\). So our full model has three parameters (like a quadratic equation \(ax^2 + bx + c\)) and our secret subspace has two parameters. In the plot below, the 3-dimensional space is restricted to a 2-dimensional plane by the projection matrix \(P \in \mathbb{R}^{3 \times 2}\). Then you can choose \(\theta^d \in \mathbb{R}^2\) and see what \(\theta^D \in \mathbb{R}^3 \) ends up as. You can also re-generate the key to generate a new secret subspace.

You can see that without the projection matrix \(P\), \(theta^d\) doesn't tell you anything about \(\theta^D\).

Let me repeat that. You cannot figure out what \(\theta^D\) is from \(\theta^d\) if you do not know \(P\). If you're not convinced, try to find \(\theta^D\) from a given \(\theta^d\) without using \(P\)!

This is the key idea of SELM: we can represent our message with \(\theta^D\), but restrain it to lie on the secret hyperplane defined by \(P\), then only send \(\theta^d\) as our ciphertext!

Aside: If you had enough pairs of \(\theta^d\) and \(\theta^D\) that came from the same matrix \(P\), you could eventually solve for \(P\) using Gaussian elimination. However, we use a standard cryptographic construction¹ to ensure that we use a different matrix \(P\) for every message sent, so you can't reconstruct \(P\) in this way.

Can Language Models Memorize Everything? [permalink]

A key question we're asked when explaining SELM is whether large language models, when restricted in their optimization to a secret subspace, can memorize all arbitrary data. While only being able to encrypt specific subsets of data is potentially useful in high-stakes situations, the more data an encryption algorithm can encrypt, the more broadly useful it is.

To find out, we encrypted lots and lots of messages from lots of different sources.

We started with GPT-2 (the 124M parameter version) from OpenAI (but Huggingface's implementation) and tried to encrypt English text that was similar to the general-domain English text GPT-2 was trained on. Specifically, we used news articles from the XSum dataset (which is not used in GPT-2's pre-training), set \(d = 10,000\) and minimized the language modeling objective until the model perfectly memorized an example with 100 tokens.

After we discovered that LMs could memorize unseen text while restricted to a subspace of the original parameter space, we investigated what factors affected the memorization speed (the number of updates to \(\theta^d\) before an example is perfectly memorized). You can (and should) read the full paper for all the details, but we tried data from different domains, data with different lengths, and different pre-trained language models.

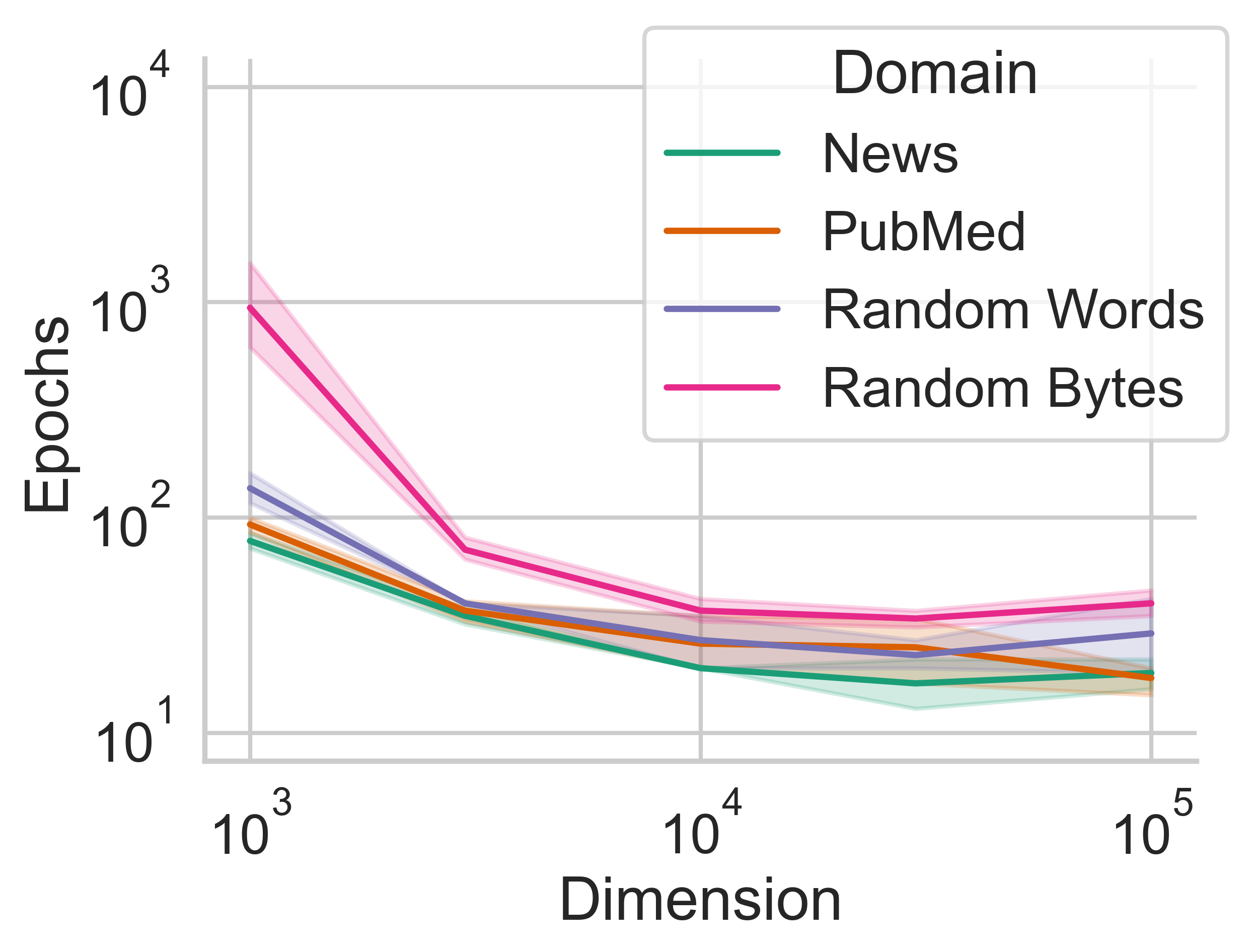
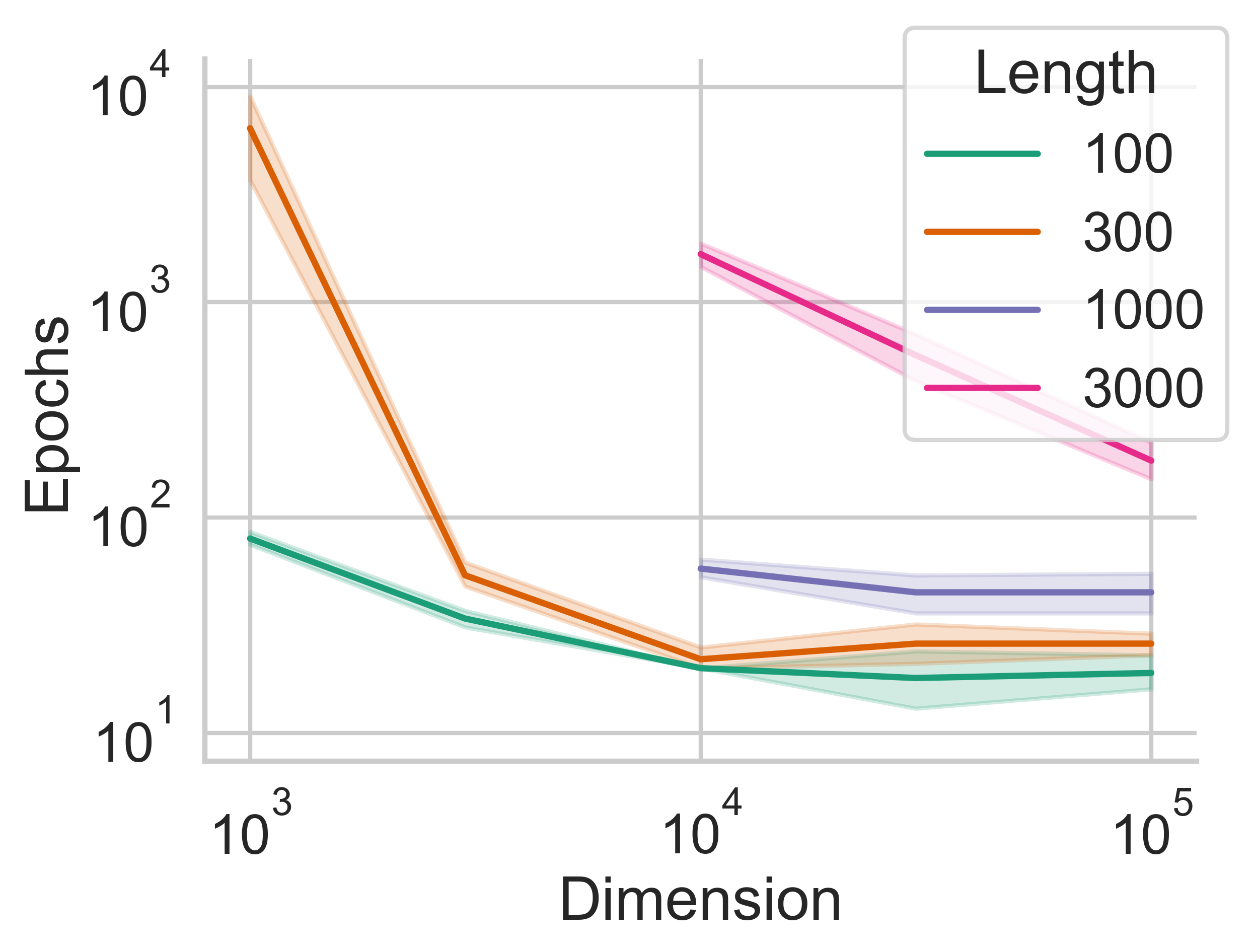
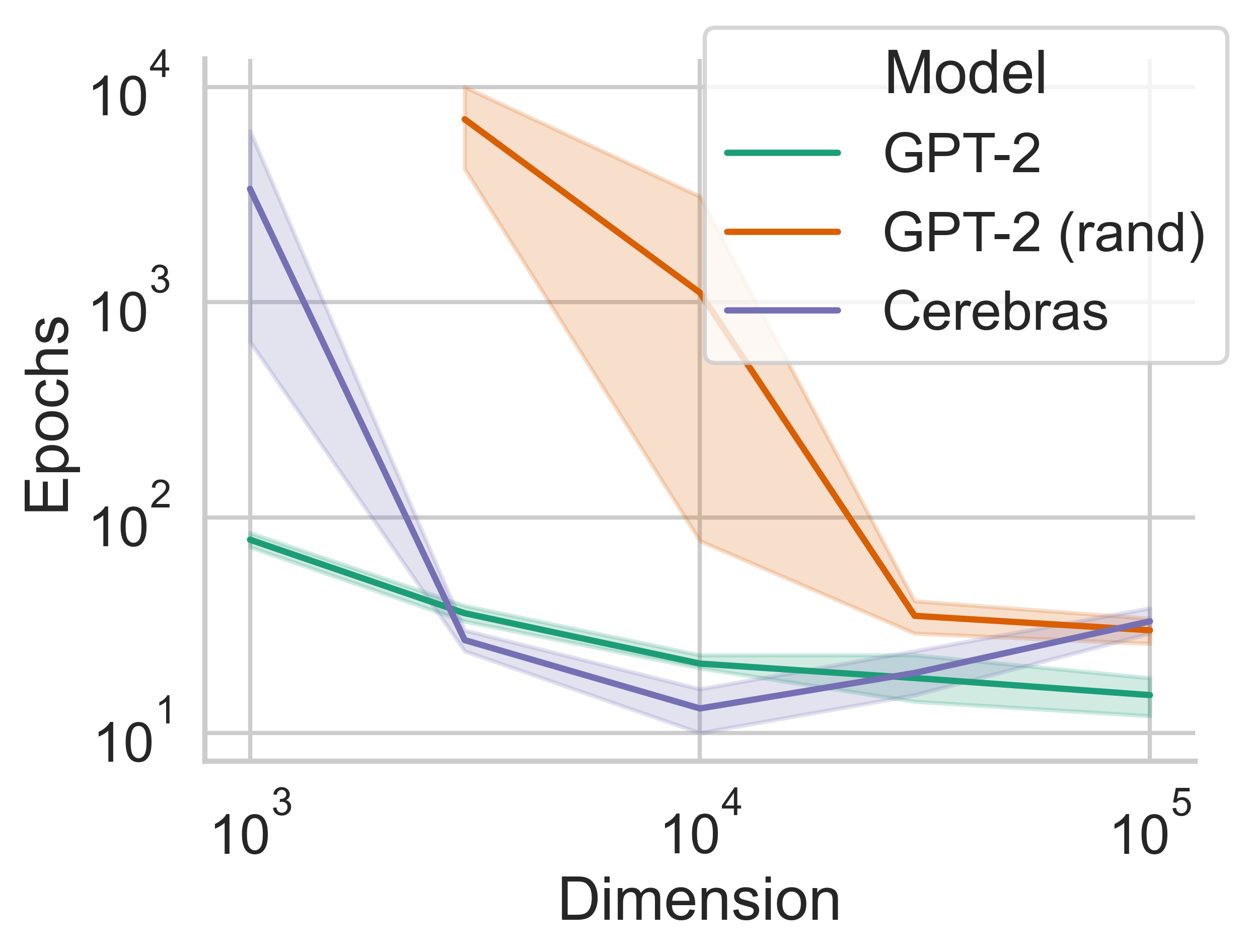
We found that:

1. Messages more similar to GPT-2's training distribution are faster to memorize.
2. Shorter messages are faster to memorize.
3. Larger values of \(D\) (more dimensions in the secret subspace) make it faster to memorize.
4. Larger pre-trained language models are faster memorizers than small, randomly initialized language models.

Amazingly, we find that language models can memorize completely random noise, even severely constrained to only a 1000 free parameters. This is a major insight into the incredible memorization capabilities learned through pre-training. Even though there is no linguistic structured in the data, a pre-trained language model can memorize data significantly faster than a randomly initialized model. This implies that pre-training teaches the model some general-purpose sequence modeling.

Semantic Security & the IND-CPA Game [permalink]

We're going to take a slight detour into a security concept: security games; specifically, the IND-CPA game.

Shafi Goldwasser and Silvio Micali proved that Alice & Bob winning the IND-CPA game means Eve cannot learn anything about the message! This makes it much easier for cryptographers. If we can just show that Eve never wins the IND-CPA game, then we don't have to worry about showing that she can't learn anything from the ciphertext.

Security games are useful strategies for cryptographers to reason about algorithm security because they enable us to focus on the absolute hardest task for an encryption algorithm. If our algorithm passes this test, it passes all the tests!

But what is the IND-CPA game? Just a series of steps.

1. Eve sends any message she likes to Alice.
2. Alice encrypts the message and sends it back to Eve.
3. Eve and Alice repeat steps 1 & 2 as many times as Eve wants to.
4. Eve sends 2 messages \(m_1\) and \(m_2\) to Alice (with the same length).
5. Alice chooses a message randomly (50/50), encrypts it and sends it to Eve.
6. Eve guesses which message was encrypted.

If Eve can guess which message was encrypted, she wins!

But even if Eve always chooses \(m_1\), she'll win half the time. So we say that Eve wins only if she gets it right more than 50% of the time.

Below, you can play as Eve against Alice with the Caesar cipher. Send messages to Alice until you think you know her key. Then send pairs of messages to Alice and guess which message she encrypted. Try to get 5 wins in a row!

Alice's key will be different every game. You can only use lowercase letters—no spaces, punctuation, numbers allowed!

Hopefully you played the game a couple times. You might have noticed that there are a couple trivial ways to win the game, where you don't need to gather any message-ciphertext pairs.

1. You give Alice two messages with different lengths. Then you can use the ciphertext's length.
2. You give Alice two messages that you already encrypted in the upper half. Then you know the exact ciphertexts for the messages you're going to submit in the lower half.
3. You use a word with two of the same letter in a row: for example, "hello" will always have the same letter in the 3rd and 4th positions.

If you didn't try any of these strategies, refresh the page and try to win without sending any messages in the top half.

These three challenges are all well-known in cryptography:

1. The IND-CPA game rules specify that Eve sends Alice two messages with the same number of characters. Cryptographers get around this challenge by outlawing it.
2. There is a well-known cryptographic construction that lets Alice choose a pseudo-random key for every message she encrypts. We use this cryptographic construction in our work.
3. This is the challenge of creating a secure cipher! This is another reason the Caesar cipher isn't semantically secure.

Is SELM Secure? [permalink]

Intuitively, we showed that without the secret projection matrix \(P\), Eve can't learn Alice's message \(\theta^D\) from the ciphertext \(\theta^d\). But can Eve learn anything? What would happen if Eve plays the semantic security game with SELM as the encryption algorithm?

Eve would:

1. Send a message \(m_i\) to Alice.
2. Receive a ciphertext \(c_i\) back.
3. Repeat steps 1. and 2. many times.
4. Send two messages \(m_1\) and \(m_2\) to Alice.
5. Receive a ciphertext \(c_?\) back.
6. Guess which message Alice encrypted (\(m_1\) or \(m_2\)).

Because the ciphertexts from SELM are high-dimensional vectors, it would be very challenging for Eve to look directly at a ciphertext and guess which message produced it. Instead, Eve could use summary statistics like the L2 norm of the ciphertext to make predictions.

Suppose Eve sends Alice the same message 500 times. Alice uses a standard cryptographic construction¹ to encrypt the message with SELM with a different secret projection matrix \(P\) each time to produce a ciphertext distribution. That is, Eve has a single message \(m\) that produced many ciphertexts. In a perfect encryption algorithm, every message's ciphertext distribution is identical. Let's see if that's true in practice.

We used 100 tokens of a news article as \(m_1\)...

Goals from Zlatko Junuzovic, Florian Grillitsch and Florian Kainz condemned second-placed Leipzig to their second successive league defeat. Bayern can extend their 10-point lead when they travel to Borussia Monchengladbach on Sunday. Borussia Dortmund closed the gap on Leipzig to three points with Friday's 1-0 win at Ingolstadt. Hoffenheim are a point further back, and boosted their chances

...and 100 tokens of random bytes as \(m_2\)...

96c2 abc2 a8c2 85c3 c257 7ea5 3313 3d1f
c25e c3be c2ba c2a2 07ab 91c3 3d51 5515
a5c2 c326 478e 402f 84c3 9cc3 c306 17bb
4a24 98c2 8ac2 3e5a adc3 bec3 abc2 c365
c2bd 67be a9c3 bac2 c27e c28c 26ba a6c2
c26d c3ba c292 c3bf 109e 8cc3 7413 c222
c394 c392 c3b7 c29d 2184 8cc2 87c2 ef3e
bdbf

(Displayed here as hexadecimal)

...and encrypted them each 400 times with SELM. Then we plotted some summary statistics of the ciphertexts. For example, for each ciphertext \(c\) we measured the L2 norm \(||c||_2\), then plotted the distributions:

The two distributions of ciphertext are extremely separable! Suppose Eve sends Alice the news article and the random bytes for step #4. If Alice encrypts the news article, the ciphertext will probably have an L2 norm that's less than 1.7e-5. If she encrypts the random bytes, the ciphertext will probably have an L2 norm that's more than 1.7e-5. This is a major security flaw that needs to be addressed.

Why does this happen? We start at the 0-vector with an L2 norm of 0, which represents GPT-2's pre-trained parameters. We hypothesize that a larger change in parameters is required to memorize messages that are dissimilar to GPT-2's pre-training corpus. That is, we have to change the parameters more to memorize random bytes compared to memorizing a news article. Because we change the parameters more, \(\theta^d\) has a larger L2 norm!

How can we fix it? We introduce a regularization term into the secret subspace optimization to reduce differences in ciphertexts. First, we add a target L2 norm: ciphertexts (\(d\)-dimensionsal vectors) need to have a target L2 norm, where the target is not zero. $$\mathcal{L}(\theta^d) = \sum_i p(t_i|t_1 \dots t_{i-1};\theta^d) + \lambda \left|||\theta^d ||_2 - \alpha\right|$$ All we did was add \(\lambda \left|||\theta^d ||_2 - \alpha\right|\), where \(\lambda\) is a hyperparameter controlling the regularization term's weight and \(\alpha\) is the target L2 norm.

We also use a regularization term that tries to minimize the difference between a ciphertext \(c\) and a \(d\)-dimensional vector \(x\) drawn from a normal distribution \(\mathcal{N}(0, \sigma^2)\): $$\mathcal{L}(\theta^d) = \sum_i p(t_i|t_1 \dots t_{i-1};\theta^d) + \lambda \int | \theta^{(d)} - x | dx $$ \(\lambda\) is a hyperparameter controlling the regularization term's weight and \(\sigma\) is the normal distribution's variance.

For each of these SELM variants (original, L2-regularization and distribution-regularization), we play the semantic security game (as humans) using the above technique with L2 norm, L1 norm, and other summary statistics. We find that both regularization techniques make it impossible to reliably win as humans. Just look at the graphs below for L2 normalization and distribution-based regularization.

We conclude that distribution-based regularization makes it very hard for Eve to win the semantic security game based on L2 norms.

But what about machines? This semantic security game is very similar to a binary classification problem:

1. Gather a training set of 800 ciphertexts, 400 with class 1 and 400 with class 2.
2. Train a model to predict a binary class attribute from a ciphertext.
3. Evaluate the trained model on some unseen test ciphertexts.

If L2 regularization or distribution regularization actually improve SELM's security, then we should see machine classification accuracy decrease!

That's exactly what we do. We use five different machine learning binary classification models, each trained on 800 examples. We evaluate their accuracy on 200 unseen examples. We model the classification models' accuracies as binomial distributions and evaluate the null hypothesis that a model is simply guessing (\(p = \frac{1}{2}\)). We reject the null hypothesis that a model is guessing for p-values less than 0.05.

A Concrete Example

For example, we train a K-nearest neighbors (KNN) classifier to predict class 1 or 2 for a 10,000-dimensional vector (the ciphertext) with 800 training examples. Then we evaluate the model's accuracy on 200 unseen examples.

Suppose it's 54% accurate. Then we check how likely it is, if we were to flip a fair coin 200 times, that we would get 54% or more heads. 54% heads out of 200 clips is 108 or more heads, which happens 14% of the time, even with a fair coin. That's common enough that we can't outright say the KNN model isn't just flipping a coin for its predictions.

If it were less than 5% likely that the KNN model is just flipping a coin for its predictions, we would reject the idea that the model is guessing and say that the only way the model could guess correctly that often is if it wasn't flipping a coin, but actually making good predictions.

Binary Classification Results

For each of the three SELM variants, we use four binary classification tasks, where each task is a new pair of messages. Message 1 is always a news article. Message 2 is either:

1. Another news article
2. A PubMed abstract
3. Random words from English Wikipedia
4. Random bytes

ALl of the messages are exactly 100 tokens long. We encrypt each message 400 times each for training and 100 times each for testing. For each ciphertext, we convert it into a vector of summary statistics to mimic the human game we played earlier. Our results are below.

SELM Variant	\(m_1\)	\(m_2\)	KNN	LDA	SVM	GradBoost	FFNN
Original	News	News	0.77	0.76	0.77	0.75	0.77
		PubMed	0.59	0.84	0.87	0.82	0.86
		Random Words	0.69	0.85	0.86	0.82	0.83
		Random Bytes	1.00	1.00	1.00	1.00	1.00
L2 Regularization	News	News	0.49	0.60	0.59	0.58	0.61
		PubMed	0.41	0.55	0.48	0.47	0.52
		Random Words	0.79	0.85	0.84	0.83	0.75
		Random Bytes	0.92	0.99	0.99	0.99	0.87
Distribution Regularization	News	News	0.46	0.49	0.52	0.51	0.46
		PubMed	0.50	0.49	0.49	0.47	0.41
		Random Words	0.48	0.47	0.49	0.45	0.47
		Random Bytes	0.47	0.45	0.47	0.58	0.55

Look how many cells are bold! That means that the classification model is learning something about the message from the ciphertext, which means SELM isn't working.

Look how few cells are bold! That means that very few classification models are learning anything from the ciphertext; SELM with distribution regularization is much more secure!

Look how KNN accuracy increases from 49% (doesn't win) to 92% (wins) as \(m_2\) goes from a news article (very similar to \(m_1\)) to random bytes (very different to \(m_1\))

Bold indicates that we reject the null hypothesis that the binary classification model is flipping a coin and assume that the model is learning something from the ciphertext, implying that SELM is not semantically secure.

Notice that stronger regularization leads to better security, and that more different message pairs are easier to distinguish. Despite the success of distribution-based regularization, the news article and random bytes are so dissimilar that gradient-boosted decision trees can still reliably distinguish the two classes.

What if we use the entire ciphertext directly, rather than using summary statistics?

Algorithm	\(m_1\)	\(m_2\)	KNN	LDA	SVM	GradBoost	FFNN
Original	News	News	0.50	0.44	0.78	0.52	0.48
		PubMed	0.50	0.49	0.81	0.54	0.57
		Random Words	0.50	0.54	0.73	0.45	0.50
		Random Bytes	0.50	0.58	1.00	0.70	1.00
L2 Regularization	News	News	0.54	0.48	0.54	0.53	0.51
		PubMed	0.48	0.58	0.50	0.49	0.49
		Random Words	0.50	0.48	0.65	0.55	0.51
		Random Bytes	0.49	0.55	0.79	0.48	0.51
Distribution Regularization	News	News	0.47	0.49	0.48	0.46	0.48
		PubMed	0.55	0.49	0.54	0.54	0.54
		Random Words	0.47	0.55	0.49	0.45	0.47
		Random Bytes	0.50	0.52	0.50	0.48	0.49

We see similar trends as before: regularization helps, but larger differences in messages lead to higher classification accuracy.

It's important to note that semantic security under chosen plaintext is one of the strongest guarantees a symmetric encryption algorithm can make. It's useful precisely because of its strictness; succeeding at this game leads to semantic security, the strongest definition of security below perfect security (which only the One-Time Pad can achieve). But failing at the semantic security game is not a death blow for symmetric encryption algorithms. Because SELM is so unlike previous encryption algorithms, there is no work explaining how to exploit a lack of semantic security to recover the key or the message. In a practical scenario, where the message space is much larger than two messages, SELM is still likely secure for many applications. But until we continue to analyze SELM, it's irresponsible to use SELM in day-to-day situations.

Why Does This Matter? [permalink]

Why does any of this matter? Why bother trying to use LMs for encryption? SELM is slower than algorithms like AES and much harder to analyze. What's the advantage over AES?

The outstanding performance of recent LLMs (e.g., ChatGPT/GPT-4) on traditional NLP tasks is calling for serious re-thinking of the scope and future of NLP research. We hope to break the mold by proposing a completely new idea for LM applications. SELM is the first work that frames LM memorization as a capability to explore, and concretly explores it under subspace optimization with the goal of developing secure symmetric encryption.

Because SELM is the very first step in this completely new direction, our results are inevitably limited in some ways. However, we believe that the cross-disciplinary nature of our work is a strength that opens up new avenues for research. With SELM, we hope to inspire further cross-disciplinary NLP works and creative applications of LMs and other NLP technologies in novel and unforeseen areas.

SELM also has important implications for the field of cryptography. Because it's based on matrix multiplication rather than Feistel networks (like DES) or substitution permutation networks (like AES), breakthroughs in cryptanalysis of DES or AES is unlikely to generalize to SELM. In fact, part of our work's novelty is trying to analyze an encryption algorithm that's isn't amenable to modern cryptanalysis like differential or linear cryptanalysis. This is especially relevant as quantum computers continue to improve. A quantum algorithm for substitution permutation networks (which would affect AES) will likely not generalize to SELM.

Thanks so much for reading! Please feel free to reach out (stevens.994@buckeyemail.osu.edu) if you have questions or comments!

Cite our work:

@misc{stevens2023memorization,
    title={Memorization for Good: Encryption with Autoregressive Language Models},
    author={Samuel Stevens and Yu Su},
    year={2023},
    eprint={2305.10445},
    archivePrefix={arXiv},
    primaryClass={cs.CL}
}

---

1: See Bourne and Stroup's A Graduate Course in Cryptography, Section 5.4.1: A generic hybrid construction.

(Optional) Beginner Introduction to Symmetric Encryption [permalink]

This section covers some basics of cryptography, including symmetric encryption algorithms, basic properties and how we measure security. You can skip it if you're familiar with the IND-CPA game.

Encryption is the outcome of cryptography, a field of math that tries to convert some readable message to an ciphertext that only the owners can read. Suppose Alice and Bob want to pass notes to each other in class about Eve's birthday gift. Alice has to pass the note to Eve, who will pass it to Bob, but only after she reads it. How can Alice and Bob communicate during class without Eve reading about their gift ideas? This is one of the many problems cryptography tries to solve with encryption. When you log in to your online banking account, for example, you only want you and your bank to see your password, not anyone else on the internet.

Symmetric Encryption [permalink]

Symmetric encryption assumes that Alice and Bob share a secret key that Eve doesn't know. In our example, Alice and Bob shared a secret key—like a password—during lunch, when Eve couldn't hear them. The symmetric encryption algorithm is actually a pair of algorithms:

1. The first algorithm (encryption) tells Alice how to turn her message into something Eve can't read: a ciphertext.
2. The second algorithm (decryption) tells Bob how to turn Alice's ciphertext (the encrypted message) back into her original message.

Both algorithms use the key as input. In a mathematical notation, encryption is a function \(E\) from messages \(M\) and keys \(K\) to ciphertexts \(C\), and decryption \(D\) is a function from ciphertexts \(C\) and keys \(K\) to messages \(M\): $$E : M \times K \rightarrow C$$ $$D : C \times K \rightarrow M$$

Decryption should be the inverse of encryption: anytime message Alice encrypts, Bob should always be able to decrypt it (assuming they have the same key). Again, formally: $$\forall m, k : D(E(m, k), k) = m$$

Caesar's cipher is a famous symmetric encryption algorithm. Alice would take every letter in her message and shift it forward by \(k\) letters. Then Bob would shift the letters back. You can play with the Caesar cipher here. Try typing in "the moon is made of cheese" with a key of 0, then a key of 1, then a key of 2.

Message:

Key: 3

Did you see what happened when you changed the key to 26? The ciphertext was the same as when the key was 0!

This is an important property of an encryption aglgorithm: the keyspace. Caesar's cipher has a keyspace of 26: there are only 26 possible keys to try. If Eve knows Alice and Bob are using a Caesar cipher, then she only has to try 26 different keys to read their message. In a long math class, there's plenty of time to try them all!

You could argue that Eve has to know that Alice and Bob are using a Caesar cipher first. If she doesn't know what the encryption algorithm is, then she won't try 26 keys. Cryptographers call this security through obscurity and it's generally regarded as a weak argument. Instead, cryptography is in favor of Kerchoff's principle: the security of an algorithm should depend only on the secrecy of the key and nothing else. That means Alice and Bob's messages should still be completely unreadable by Eve even if Eve knows the algorithm, the time of day, the weather—anything and everything except the key and the original message.

The big question is: How do we measure the security of an algorithm?

Security

Remember, Alice and Bob want to send each other messages without Eve being able to read them. More than that, Alice and Bob want to send messages without Eve learning anything at all about them.

Why does it matter if Eve can learn anything, if she can't read the whole message? Suppose that Eve knows that Alice and Bob are choosing between getting Eve a bunny, a goose, a horse or a snake for her birthday (Eve really likes animals!). If Alice and Bob are using a Caesar cipher with an unknown key, can Eve figure out which animal they're getting?

Suppose Eve knows that Alice and Bob are going to get her a snake 1 in 20 times, a horse 1 in 10 times, a goose 1 in 5 times and a bunny the rest of the time. Then Eve can plot those probabilities as a pie chart (on the left).

If Alice sends the word "goose" with a key of 3, then the ciphertext is "jrrvh" (try it on the Caesar cipher demo above!). Even though Eve doesn't know the key, since "goose" is the only word where the second and third letters are the same, she knows that "jrrvh" must be "goose"!

If Alice sends the word "snake" with a key of 4, the ciphertext is "wreoi", which doesn't have any repeating letters in it. So Eve isn't sure if it's "snake" or "horse", but she does know she's not getting a goose or bunny for her birthday! Once she removes the goose and the bunny from the pie chart, she gets the chart on the right (After Ciphertext). Even though Eve can't understand the ciphertext, she's learned something! In a perfect encryption algorithm, the two pie charts would always be the same.

You can play with the different keys and messages in the demo below and see what Eve can learn.

Choose a message:

snake horse goose bunny

Key: 3

You can see that the Caesar cipher isn't helping Alice and Bob much because Eve can learn from the ciphertext. Then how do we make sure our algorithms don't leak any information to Eve? That's covered above, in the semantic security section. Go read the rest of this post to find out about semantic security and SELM!