Jupyter Notebooks for Engineering Classes

I have one more “traditional” engineering class in my time at Ohio State which is ECE 2020: Introduction to Analogue Circuits. I took digital circuits a couple semesters ago, and that class was basically boolean expressions but with little lines connecting to boxes. This class is more resistors/inductors/capacitors/I never took a class on complex numbers oh God. So, there’s a little more algebra involved, and it becomes especially unwieldy when we start using complex numbers for the phasor domain.

But I knew there were symbolic solvers out there (Wolfram Alpha, for one), and I was feeling more comfortable with Jupyter notebooks, so I decided to use Sympy to do all of my homework for ECE 2020 in a notebook.

Here’s how I set it up:

1. Set up a virtual environment (preferably in Python3)
2. Install iPython, Jupyter and Sympy
3. Create a notebook
4. Use Sympy and cmath to solve the hard problems

Setting up a Virtual Environment

Assuming you have python3 installed on your machine (if you don’t, look here (or anywhere on the internet) for instructions):

cd <your school folder>
python3 -m venv school-venv
. school-venv/bin/activate

Installing Dependencies

We need Jupyter and Sympy (Jupyter will install iPython as a dependency):

pip install jupyter sympy

Then we need to create a kernel for Jupyter that corresponds to this virtual environment:

. school-venv/bin/activate
ipython kernel install --user --name=school

Create a notebook

jupyter notebook <your school folder>

This will launch the web interface. From here, I navigate to my class folder and create a new notebook with my school kernel

Solve Problems

I always import Sympy and exp from cmath, and set up j to mean 0+1j:

import sympy as sym
from cmath import exp
j = 1j # for convenience

And here’s an example of how I would do an ECE problem:

First, set up my constants.

w = 300
z1 = 8
z2 = 8
v = 1+0j
i = 2+0j

Next, I set up values that depend on constants.

zL = j * w * 3 * 10 ** -6
print('zL:', zL)

zTH = 1 / (1/z1 + 1/(zL + z2))
print('zTH:', zTH)

zC = -j / (300 * 5 * 10 ** -6)
print('zC:', zC)

Finally, I use Sympy to solve for variables in multiple equations.

Note: You need to set up Va and Vc as sym.Symbol() for Sympy to solve for it.

Note 2: The results from Sympy are not type complex; they must be cast before being used with other complex numbers, or you end up with weird results.

Va = sym.Symbol('Va')
Vc = sym.Symbol('Vc')

result = sym.solve(
    (
        (Va - v) / z1 + (Va - Vc) / zL,
        (Vc - Va) / zL + Vc / z2 - i
        # as far as I know, these equations are always assumed to equal 0
    ),
    (Va, Vc)
)
vTH = complex(result[Va])
print('vTH:', vTH)

And this is how it all might look within a Jupyter notebook:

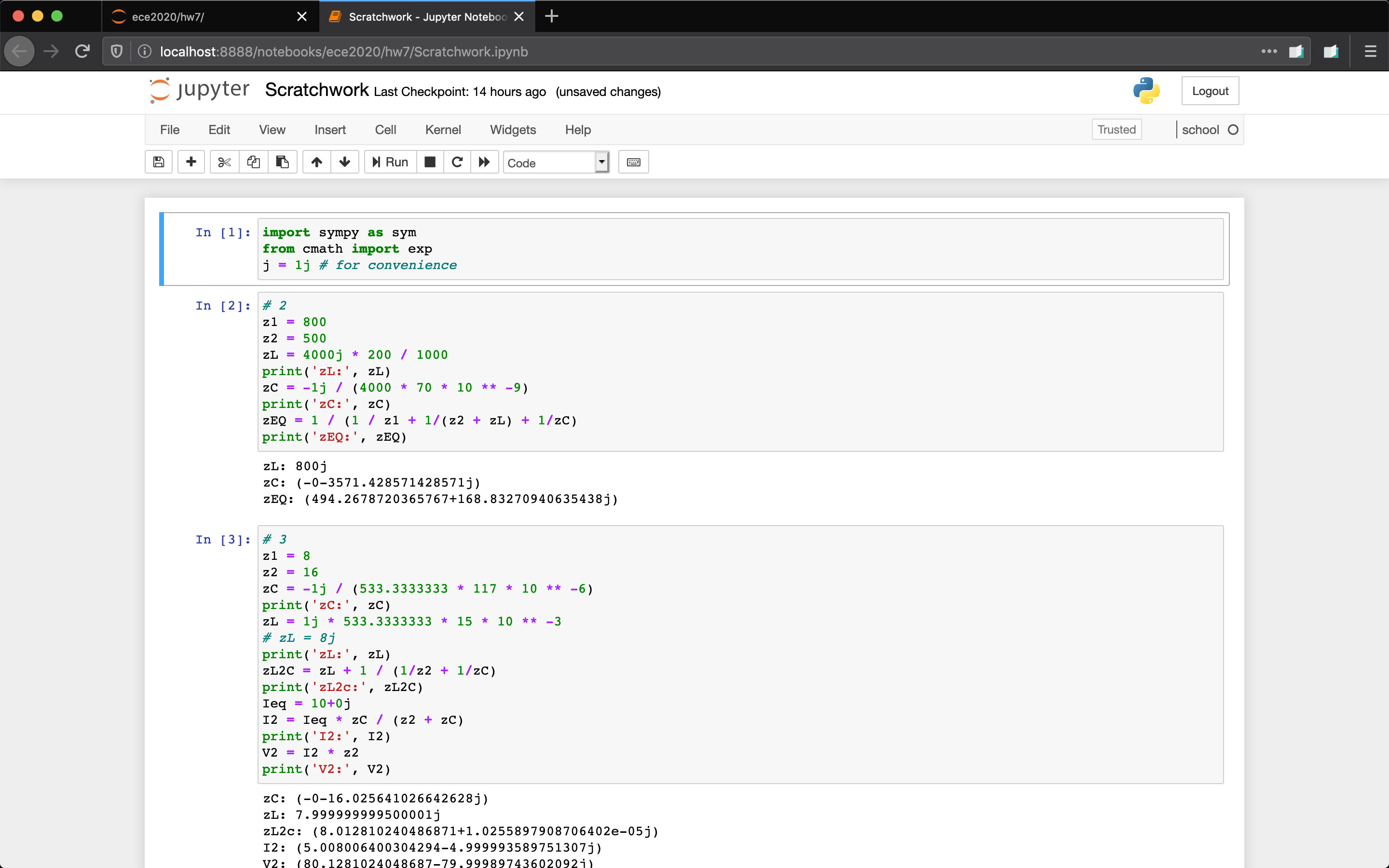
This is how I avoid doing any hard math in my ECE class.

Please email me if you have any comments or want to discuss further.

[Links] [Source]

Sam Stevens, 2024